非線形波動の物理/特性曲線法を用いた非線形波動方程式の解法（例題1.1）

一般的な波動方程式

$$\frac{\partial \rho}{\partial t} + c(\rho)\frac{\partial \rho}{\partial x} = 0$$

では，伝播速度$c$が従属変数$\rho$の関数になっている．

このため，この式は$\rho$の一次式ではなく，非線形偏微分方程式となっている．

非線形波動方程式の初期値問題は，以下のような手順で解く．

$\rho$の初期分布から$c$の初期分布を求める
$x$軸上の任意の点$(x,t) = (\xi,0)$を通り，傾き$c_0(\xi)$の直線$x=\xi+c_0(\xi)t$を引く．これが特性曲線となり，この上で$\rho$は一定値$\rho_0$をとる．
この時，時刻$t$における$\rho(x,t)$の波形は，特性曲線の出発点$\xi$をパラメタとするパラメタ表示

$$\rho(\xi)=\rho_0(\xi), x(\xi)=\xi+c_0(\xi)t$$

で与えられる．

特性曲線法に基づいて，以下のような非線形波動方程式の初期値問題を解く．

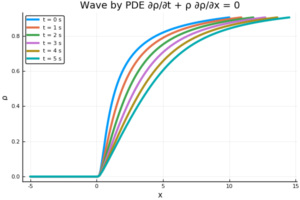
$$\frac{\partial \rho}{\partial t} + \rho\frac{\partial \rho}{\partial x} = 0$$

$$-\infty < x < \infty, t > 0$$

\begin{eqnarray} \rho = \begin{cases} 0 & ( x \le 0 ) \\ \exp{(-1/x)} & ( x \gt 0 ) \end{cases} \end{eqnarray}

$t = 5$における$\rho(x,t=5)$の波形をかけ．

波の出発点になる$x=\xi$を適当に設定する．今回は，$-5 \le \xi \le 10$に設定．
与えられた$\rho$を設定する．
波速$c=c(\rho)$を計算する．今回は，$c=\rho$となっている．
各出発点$\xi$から出発する特性曲線が，$c(\xi)$という速さで$t=5$に到達する$x$座標を求める．$x = \xi+c(\xi) \times 5$で計算可能．

0から5sまでのすべての波形を描いた．（2019/10/01，図面を修正）